Predictions

The calculation simulates the experimental situation, where the crystal intensity is obtained from bremsstrahlung off a diamond radiator. In fig. 1 the absolute intensities from an amorphous (nickel) and a crystal radiator (diamond) are plotted to demonstrate what can be expected from tagging efficiency measurements. The incoherent contribution used for the relative intensity in fig. 2 stems from a nickel radiator in order to allow a comparison to a measured relative intensity. The total crystal intensity is the sum of the coherent and incoherent contribution from diamond, whereas the latter must be distinguished from the incoherent intensity of nickel, which is generally the measured one.

  

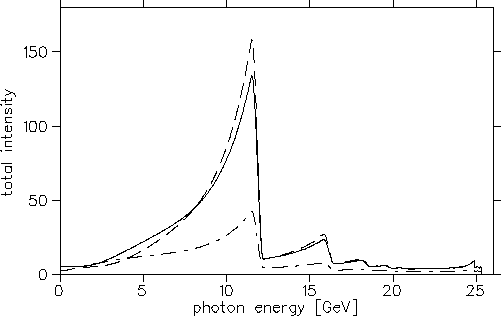
Figure 3: Prediction of abspolute intensity for set B (dot-dashed), C (solid) and D (dashed).

From the intensity the cross section per atom is calculated via: 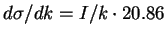$d\sigma/dk = I/k \cdot 20.86$ mbarn, with k being the photon energy. Note that the relative intensity (dashed line in fig. 2) 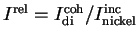$I^{\text{rel}} = I^{\text{coh}}_{\text{di}}/I^{\text{inc}}_{\text{nickel}}$ is scaled by a factor of 0.05. The linear polarisation is plotted in fig. 2 reaching a maximum polarisation of about 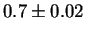$0.7\pm 0.02$ in the energy region of 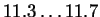$11.3\ldots 11.7$ GeV. On a target, which is for example 10 m afar, 90% of the photon beam would be contained within a circular area of 2.2 mm radius. The results for three sets (B,C,D) of parameters in tab. 2 are shown in figs. 3 and 4.

  

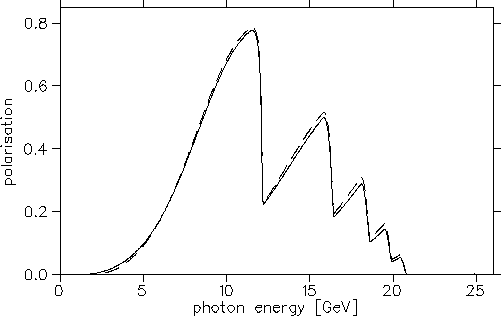
Figure 4: Prediction of polarisation for set C (solid) and set D (dashed). Set B results in similar polarisation than in cases C and D.