Collimation

The angular distribution of the coherent contribution is always narrower than the incoherent one (here 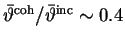$\bar\vartheta^{\text{coh}}/\bar\vartheta^{\text{inc}} \sim 0.4$). Therefore for an ideal electron beam and a very thin target, the collimation of the photon beam enhances the polarisation whenever the collimation angle is in the order of the mean polar angle of the coherent photon beam. In general experimental deficiencies deplete the maximal photon polarisation. This can be compensated by collimation if the electron divergence and beam spot size is small compared to the collimator angle. In the sense that the area being swept by the photon beam is about the size of the collimator area. For a rough estimate the opening angle of the beam spot viewed from the collimator must be less than half the collimator angle. Therefore an increase of collimator distance reduces this opening angle.

 

Table 2: Collimation and photon beam properties

set	beam spot	colli/target	colli	maximal	tagging
	($\sigma_s$) [mm]	distance [m]	radius	polarisation	efficiency
A	1	10	uncoll	.74	1
B	1	10	0.6	.75	.15
C	1	50	1.5	.77	.30
D	0.1	10	1.2	.78	.30

The parameters given in tab. 1 do not meet the above requirement, because the polar angle distributions of incoherent and coherent contribution have the same widths, hence a collimation is not advisable. Furthermore the sizable electron beam divergence and large beam spot size on the radiator leads to a strongly reduced tagging efficiency, see calculation of set B in tab. 2. Especially the large beam spot size necessitates to place a collimator at least 50 m downstream the radiator for a significant enhancement of the polarisation.

  

Figure: Prediction of relative intensity $\left . I^{\text {rel}}=I^{\text {coh}}_{\text {di}} \right / I^{\text {inc}}_{\text {nickel}}$ (multiplied by .05, dashed) and photon polarisation without collimation (set A).

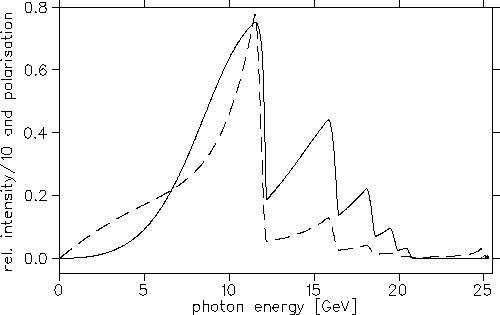The calculations show, that the gain in polarisation will not balance the smaller photon flux (set C in tab. 2 and fig. 3). A significant reduction of the beam spot size (set D) would be more promising. With very different beam and collimation parameters (set C and D) one can obtain similar cross sections and polarisations.